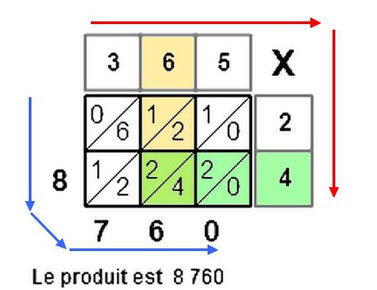
Multiplication à la grecque
La multiplication à la grecque
- Dans chaque case on note le produit du nombre de la première ligne par celui correspondant dans la colonne de droite.
- Il suffit de bien connaître ses tables.
- Pour le résultat final, on ajoute en DIAGONALE en tenant compte des retenues additives, les résultats obtenus dans les cases et ceci de droite à gauche.
- Les diagonales sont marquées par les traits obliques coupant les cases en deux.
- Bien entendu on ne prend ni la première ligne ni la colonne de droite contenant les nombres de départ.
Elle présente de nombreux avantages :
- Pas de retenues multiplicatives à mémoriser ;
- Pas de problème de décalage de ligne ;
- On peut s'arrêter et reprendre à tout instant ;
- Aucune difficulté pour les zéros intercalés comme dans 205.
- Le tracé des lignes peut se faire à main levée.
- Et si l'on se trompe, on retrouve très vite l'erreur.
- On voit également sans problème si l'erreur est due au manque de connaissance des tables ou à une méconnaissance de l'algorithme.
Histoire
Cette merveilleuse technique nommée aussi italienne ou grecque qui nous vient d'Orient est utilisée au XVème siècle par le mathématicien arabe Al kasi, ![]() . Mais on la trouve beaucoup plus tôt chez les arabes aux
alentours du XIIIe siècle (multiplication par le quadrillage ou par le tableau).
. Mais on la trouve beaucoup plus tôt chez les arabes aux
alentours du XIIIe siècle (multiplication par le quadrillage ou par le tableau).
Elle serait dans un ouvrage de Fibonacci de 1202.
A la fin du Moyen-Age la technique fut surnommée "per gelosia".
Ce nom fait allusion à la pièce en bois qui équipait certaines "fenêtres à jalousie" en Italie chez les maris jaloux. Ils voulaient bien que leur femme regarde ce qui se passe dans la rue, sans
que les hommes qui s'y trouvaient pussent la voir.
Cette technique a fini par donner notre algorithme de multiplication.
 Ecole Haut-Poirier 2024/2025
Classe CM2
M.WIEDERKEHR
Ecole Haut-Poirier 2024/2025
Classe CM2
M.WIEDERKEHR